Bokeh Charakter bestimmen

Über das Bokeh von Objektiven wird mittlerweile genauso leidenschaftlich diskutiert wie über das Bouquet von Weinen - dem einen gefällt es, dem andere nicht. Dennoch ist es so, dass bei manchen Objektiven das Bokeh - der unscharfe Bereich, unruhig wirkt.

Die spannende Frage ist dabei - was ist der Auslöser dafür? Die pragmatische Antwort darauf: der Charakter des Zerstreuungskeises definiert den Charakter des Bokeh’s.

Der Zerstreuungskreis ist die Betrachtung eines lokalen Phänomens - des Verhaltens der von einer punktförmigen Lichtquelle ausgehenden Strahlen durch ein optisches System.

Bei der Beurteilung des Bokeh’s betrachten wir dagegen des Gesamtbild - die Abbildung der gegenständlichen Welt auf einer Bildebene/Sensor. Hierbei überlagern sich unterschiedliche Zerstreuungskreise.

Sphärische Aberration und der Zerstreuungskreis

Traditionell sind die Linsen in Objektiven geometrisch gesehen Schnitte von Kugelflächen (Sphären). Lichtstrahlen, die durch Sphären gebündelt werden, haben keinen klaren Brennpunkt, da die Strahlen, die durch Rand der Linse laufen stärker gebrochen werden und dadurch einen Brennpunkt näher an der Linse haben:

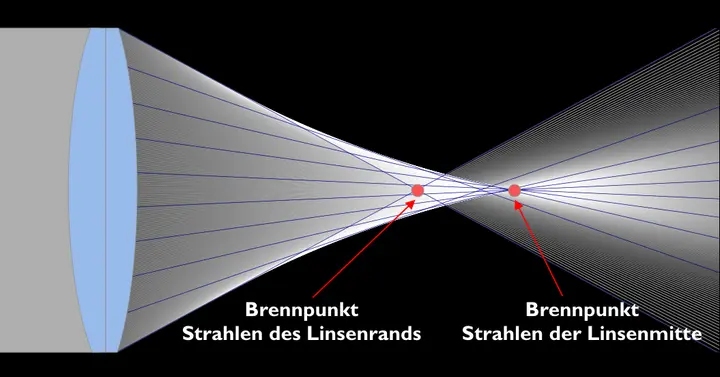
Das hat Konsequenzen für die Zerstreuungskreise. Je nach Abstand des Sensors von der Linse ergeben sich unterschiedliche Arten der Zerstreuungskreise:

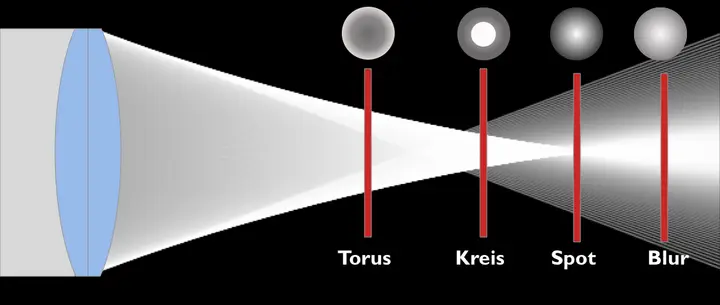
Liegt der Brennpunkt vor der Bildebene/dem Sensor (von der Linse aus gesehen), wird der Zerstreuungskreis zum Torus/Donut. Liegt der Brennpunkt hinter der Bildebene (von der Linse aus gesehen), wird der Zerstreuungskreis zum Softspot oder Blur.

Diese Effekte lassen sich minimieren durch Verkleinerung der Blende (dadurch werden die Randstrahlen abgeschnitten), oder durch den Ersatz der sphärischen Linse durch eine asphärische Linse. Bei Sphären ist das Krümmungsverhalten der Linsenoberfläche immer gleich, bei Asphären nimmt das Krümmungsverhalten zum Rand hin ab. Randstrahlen werden dadurch weniger stark gebrochen und haben denselben Brennpunkt wie die Strahlen, die durch die Mitte der Line gehen.

Für die konkrete Situation einer fotografischen Aufnahme hat das Konsequenzen, da sich der Bokeh Charakter unterscheidet, je nachdem, ob sich die unscharf abgebildeten Gegenstände im Vordergrund (zwischen Kamera und scharf gestelltem Motiv) befinden, ob diese im (unscharfen) Hintergrund liegen.

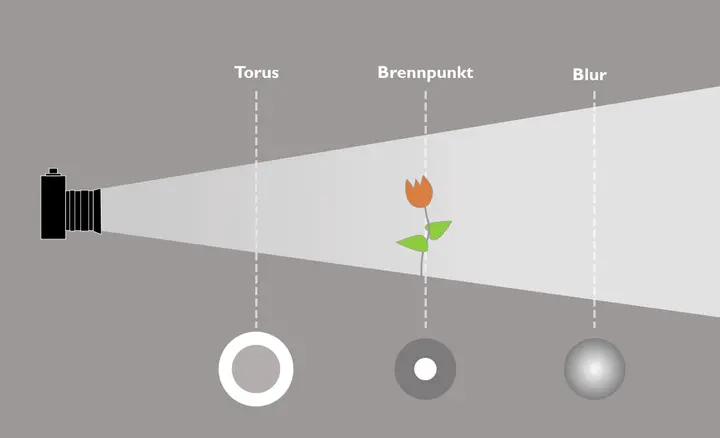
Dieser Sachverhalt ist der Grund, dass ein Linsenkonstrukteur nicht gleichzeitig das Bokeh auf den Vordergrund und den Hintergrund optimieren kann.

Kritische Situationen

Problematisch sind vor allem Situationen, bei denen sich die Zerstreuungskreise verschiedener abgebildeter überschneiden und dadurch neue geometrische Muster auf dem Sensor erzeugen.

Diese Situation kann man ganz gut mit dem Siemensstern simulieren; beim Siemensstern haben wir zentrisch zulaufende Linien mit harten Kontrasten.

Lizenzhinweis: Der Siemensstern wurde als SVG von https://de.wikipedia.org/wiki/Siemensstern#/media/Datei:Siemens_star.svg heruntergeladen und steht unter der http://creativecommons.org/licenses/by-sa/3.0/ Lizenz. Alle hier abgebildeten Bilder stehen demnach ebenfalls unter der CC-BY-SA Lizenz.

Das Foto wurde mit der Fuji X-E4 (APS-C Crop Sensor) und dem 50mm Objektiv bei Offenblende 2.0 aufgenommen. Kanten werden hierbei durch sanft geblurrte Verläufe abgebildet. Liegen die Kanten nahe genug beieinander, so überschneiden sich die Zerstreuungskreise und ergeben neue geometrische Muster.

Interessant ist bei diesem Bild der mittlere Bereich. Die Kanten des Siemenssterns überlagern sich so stark, dass die Helligkeiten invertieren.

Solche Strukturen ziehen die Aufmerksamkeit auf sich, man könnte auch sagen - sie lenken ab. Wenn wir Unschärfe einsetzen wollen, um das Motiv von der Umgebung zu separieren, ist das kontraproduktiv - denn der nebensächliche Hintergrund wird zum Eye-Catcher.

Simulation des Bokeh’s anhand des Zerstreuungskreises

Ich hab nun versucht das optische Verhalten in einem Softwareprogramm zu nachzubilden, denn hierüber bekomme ich die Freiheit, mir Zerstreuungskreise konstruieren und ihre Auswirkung auf das Bokeh simulieren zu können. Ziel ist nicht die exakte Nachbildung, sondern der gewinn an Verständnis über die Zusammenhänge.

Bokeh Simulation findet sich in jedem Bildverarbeitungsprogramm mit der Blur Funktion. Hierbei werden benachbarte Pixel zusammengerechnet. Üblicherweise wird hierbei nicht der einfache Mittelwert der Pixel genommen, sondern das gewichtete Mittel einer Gauß-Verteilung.

Mathematische Beschreibung

Mathematisch gesehen handelt es sich hierbei um die Faltung (Convolution) zweier Funktionen.

Die mathematische Beschreibung der Faltung lautet:

$(f * g)(x) = \int f(\tau) \cdot g(x-\tau) d\tau$

Die Funktion f beschreibt hierbei das eigentliche Bild, die Funktion g (der Kernel) beschreibt die Gewichte. Die Integralfunktion beschreibt hierbei die Aufsummierung aller Kombinationen $f(\tau) \cdot g(x-\tau)$

Algorithmische Umsetzung

In der algorithmischen Umsetzung summieren wir nur einzelne Werte auf. Das Verfahren ist anschaulich ziemlich einfach; jeder Bildpunkt wird mit einem korrespondierendem Gewichtswert multipliziert.

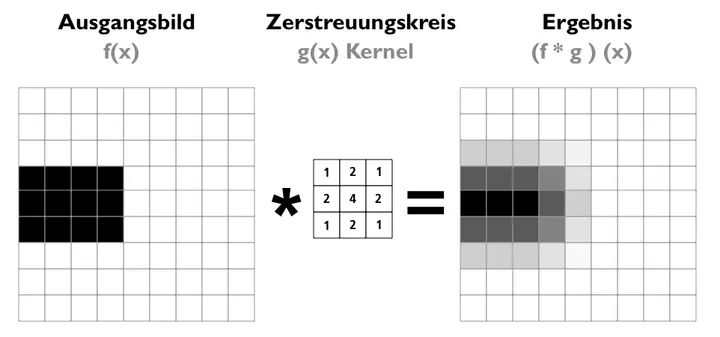
_Anmerkung: obiges Bild ist vereinfacht dargestellt (die Summe der Werte des Kernels muss 1 betragen - hier hab ich es weggelassen aus Gründen der Anschaulichkeit: Man erkennt besser, dass der mittlere Punkt 4-fach in die Wertung eingeht, während der Rand- bzw Eckwerte nur 2- bzw. 1-fach).

Vergleich verschiedener Zerstreuungskreise und Auswirkung auf das Bokehverhalten

Zum Vergleich habe ich unterschiedliche Zerstreuungkreise simuliert und auf jeweils zwei Bilder angewendet - den Siemenststern und ein scharfes Foto mit starken Kontrasten. Die Fotos wurden auf jeweils 1000 x 666 Pixel heruntergerechnet und mit einem Zerstreuungskreis-Kernel von 30x30 Pixel modifiziert.

Der Zerstreuungskreis-Kernel entspricht damit etwa 3% der Bildbreite. In der realen Welt ergeben das bei einer APS-C Kamera mit 24 Megapixeln eine Zerstreuungskreis von etwa 0,8mm; diesen Zerstreuungskreis erhält man beispielsweise für unendlich weit entfernte Gegenstände mit einem 50mm, f2 Objektiv, scharfgestellt auf ungefähr zwei Meter.

Ein (für meine Begriffe) schönes Bokeh. Der Zerstreuungskreis wurde konstruiert mit einem quadratischem Lichtabfall von der Linsenmitte zum Rand hin.

Hier wurde der Zerstreuungskreis als Donut konstruiert mit einem scharfen Rand. In dieser Form vermutlich übertrieben, aber eine gute Demonstration des daraus resultierenden unruhigen Bokeh’s. Das Donut Bokeh ist das Gegenstück des Blur Bokeh’s; tritt das eine im Hintergrund auf, dann das andere im Vordergrund.

Hier ist der Zerstreuungskreis eine Scheibe (nicht and er pixeligen Darstellung stören, diese hat auf das Verhalten keinen nennenswerten Einfluss. Dieses Verhalten erhält man typischerweise beim Einsatz von asphärischen Linsen, um den oben beschrieben Fehler der sphärischen Aberration zu korrigieren.

Fazit

Unter idealisierten Bedingungen ergeben nicht asphärisch korrigierte Objektive ein harmonischeres Bokeh im Hintergrund. Man darf sich also entscheiden. Asphärische Linsen dagegen bringen hohe Schärfe, aber unter Umständen unschöne Unschärfe sowohl im Vordergrund als auch im Hintergrund.