Fokusdistanz bei Zwischenringen

Berechnung der maximalen Fokusdistanz bei Zwischenringen und Makroadaptern wie dem MCEX-11

Ich habe den Makroadapter MCEX-11 für das Fuji X System. Welches Objektiv sollte ich damit verwenden? Reine Makroobjektive sind eher ein Tele, bei Fuji z. B. 60 mm oder 80 mm.

Mit einem 50mm muss ich schon mindestens 20cm nah ran; bei dem 16mm-Weitwinkel kann ich nämlich nur Objekte fotografieren, die sich direkt vor der Frontlinse befinden – das ist verdammt nah. Blende ich ab, kann ich den Staub auf der Frontlinse fotografieren :-)

Aber woran liegt das genau? Intuitiv klar ist, dass das Verhältnis von 11mm (denn genauso lang ist der MCEX-11) zu einem 16mm Objektiv deutlich größer ist als das Verhältnis von 11mm zu 60mm. Aber kann man die maximale Fokusdistanz und den Abbildungsmaßstab berechnen?

Genau das werden wir hier machen.

Abbildungsmaßstab und Fokusabstand berechnen

Die Formeln hängen nur von der Brennweite (f) und der Tiefe des Zwischenrings (∆b) ab.

Die Formel zur Berechnung des Abbildungsmaßstabs (M) lautet:

$$ M = \dfrac{\Delta b}{f} $$

Die Formel zur Berechnung der maximalen Fokusdistanz (g) lautet:

$$ g = f \cdot \left(1 + \dfrac{f}{\Delta b}\right) $$

Interessanterweise beschreibt der Quotient ∆b/f bzw f/∆b in den beiden Gleichungen genau das, was auch intuitiv eine Rolle spielt: das Verhältnis der Länge des Zwischenrings zur Brennweite.

Die Formeln gelten strebg genommen nur für einzelne Linsen. bei komplexen optischen Systemen wie modernen Objektiven wird die Berechnung schwieriger; das lassen wir an dieser Stelle mal einfach beiseite. Uns interessieren ja mehr die grundsätzlichen Zusammenhänge.

Beispielrechnungen für einen Zwischenring mit 11 mm (MCEX-11)

Das ergibt für die folgenden Brennweiten die Ferneinstellgrenzen:

Gerundete Werte. Der Entfernungsring des Objektivs ist auf Unendlich gestellt. Die Ergebnisse weichen von den gemessenen Werten ab, da - wie schon angemerkt - die Formeln für einzelne Linsen und nicht Linsensysteme gelten. Nimmt man bei dem 16mm die Mitte des Objektivs als Zentrum, so sind die berechneten 4 cm Abstand sehr nah an der Frontlinse dran…

Herleitung der Rechenformeln

Wenn ich einen Makro-Zwischenring wie den MCEX-11 einsetze, vergrößere ich den Abstand von Objektiv zum Sensor. Dadurch verschiebt sich die Schärfeebene – und der Abstand des scharf abgebildeten Objekts zur Linse rückt näher an die Kamera heran. Genau das passiert ja auch beim normalen Fokussieren ohne Zwischenring: Man schiebt das Objektiv über einen Schneckengang heraus, die Schärfe wandert näher heran. Mit einem Zwischenring vergrößert man diesen Auszug zusätzlich.

Hinter diesem Verhalten steckt eine einfache Regel:

Vergrößert sich (mit einem Zwischenring) die Bildweite b, verkürzt sich die Gegenstandsweite g.
Die Gegenstandsweite ist Abstand der Schärfeebene von der Linse
Die Bildweite ist der Abstand der Linse zum Sensor

Die mathematische Beziehung lautet:

$$ g = \dfrac{b \cdot f}{b - f} \qquad (1) $$

Diese Gleichung ergibt sich direkt aus der klassischen Linsengleichung:

$$ \dfrac{1}{f} = \dfrac{1}{g} + \dfrac{1}{b} \qquad (2) $$

Die Linsengleichung lässt sich geometrisch über ähnliche Dreiecke ableiten. Dabei ergibt sich als schöner Nebeneffekt auch die Grundregel für den Abbildungsmaßstab (M):

$$ M = \dfrac{B}{G} = \dfrac{b}{g} \qquad (3) $$

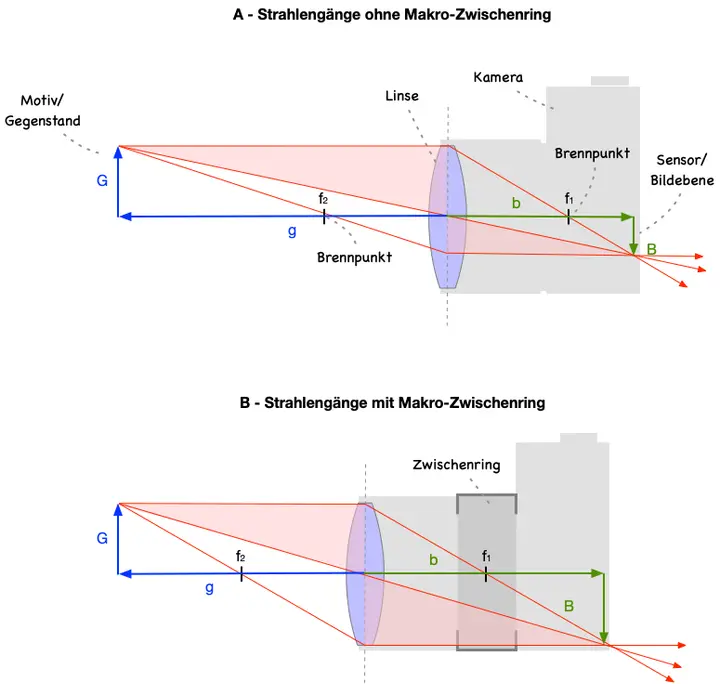
Herleitung der Formel für den Fokusabstand

Wenn das Objektiv auf Unendlich gestellt ist, gilt:

$$ b = f + \Delta b $$

Eingesetzt in die Formel (1):

$$ g = \dfrac{(f + \Delta b) \cdot f}{\Delta b} = f \cdot \left(1 + \dfrac{f}{\Delta b}\right) $$

Herleitung des Abbildungsmaßstabs

Der Abbildungsmaßstab (M) beschreibt das Verhältnis zwischen Bildgröße und Objektgröße:

$$ M = \frac{B}{G} $$

Geometrisch ergibt sich dieser Maßstab auch aus dem Verhältnis der Bildweite (b) zur Gegenstandsweite (g):

$$ M = \frac{b}{g} $$

Setzt man die Formel für (g) ein:

$$ g = \frac{b \cdot f}{b - f} $$

dann ergibt sich:

$$ M = \frac{b}{\frac{b \cdot f}{b - f}} = \frac{b - f}{f} $$

Wenn das Objektiv auf Unendlich eingestellt ist, gilt:

$$ b = f + \Delta b \Rightarrow b - f = \Delta b $$

Daraus folgt:

$$ M = \frac{\Delta b}{f} $$

Diese elegante Formel zeigt: Der Abbildungsmaßstab ist direkt proportional zur Tiefe des Zwischenrings und umgekehrt proportional zur Brennweite.

Lichtverlust durch Zwischenringe

Ein Nachteil von Zwischenringen ist, dass sie – im Gegensatz zu echten Makroobjektiven – einen Lichtverlust mit sich bringen. Das bedeutet, man muss länger belichten.

Der Verlängerungsfaktor ist sehr einfach zu berechnen:

$$ \text{Verlängerungsfaktor} = \left(\frac{b}{f}\right)^2 $$

Und mit $$ b = f + \Delta b $$ ergibt sich $$ = \left(1 + \frac{\Delta b}{f}\right)^2 $$ Der Verlängerungsfaktor wächst also quadratisch mit dem Auszug.

Beispielhafte Verlängerungsfaktoren:

Praktisch heißt das: Bei den typischen Makrobrennweiten (80 mm bei APS) hat mein einen vertretbaren Lichtabfall, der automatisch von Digitalkameras berücksichtigt wird. Bei manuellen Kameras ohne TTL muss man den Faktor in die Belichtungssteuerung mit einbeziehen.